对于交易来说，胜率和盈亏比，哪个更重要？

当你具备了系统化交易的思维之后，不会面临胜率和盈亏比的取舍问题。俗话说“鱼与熊掌不可兼得”，高胜率和高盈亏比只能二选一。

初出茅庐的人充满幻想，他们坚信高胜率和高盈亏比可以同时存在。以COMEX黄金为例，3月份累计交易了20笔，其中2笔交易亏损，18笔交易盈利，平均每笔亏损额100美元，平均每笔盈利额500美金。

如此一来，胜率高达90%，盈亏比高达5倍，堪称完美。不可否认，这种情况确实存在，但是，只存在于短周期之内。拉长周期来看，胜率和盈亏比一定是跷跷板关系。

为了定量分析这种反向关系，我们引入“期望值”这一同一学概念。

期望值的专业定义是：在一个离散性随机变量试验中每次可能结果的概率乘以其结果的总和。通俗的定义是：每笔交易单的平均获利金额。以上文提到的20笔交易为例：平均盈利为500美金，盈利概率为90%；平均亏损为100美金，亏损概率为（1-胜率）=10%。所以，3月份COMEX黄金的最终交易期望值为：500*90%-100*10%=450-10=440美元。

每笔交易的期望值可以达到440美元，如果你认为这种交易结果可以长期存在，那么砸锅卖铁也要扩大资金参与。假如你真的这样做了，等待你的极有可能是巨额亏损，甚至于爆仓。为什么？因为胜率和盈亏比是跷跷板关系，交易的期望值往往在零附近徘徊！

让我们回归现实吧。当平均盈利金额是500美金，平均亏损金额为100美金时，合理的胜率是多少？通过期望值公式的逆推即可得出。假设胜率为P，则500*P-100*（1-P）=0，计算可得，P=1/6=16.667% 。

也就是说，在五倍盈亏比之下，经历过足够多次的交易后，胜率会不断向16.667%回归，失败的概率则向83.333%回归。当然，如此计算的前提是COMEX黄金的价格是纯粹的随即波动，只有这样期望值才会是零。现实情况下，黄金价格并不是纯粹的随机波动，它存在与宏观经济的共振性。但是，这种非随机性在长周期价格走势中表现更明显，获利难度相对较小；对于小时/分钟级别的价格波动，则随机性更强，获利难度更大。

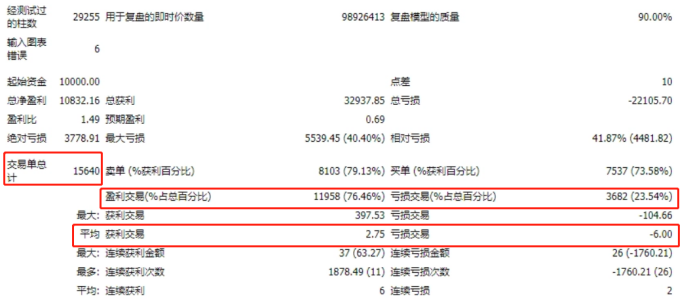
如上图所示的交易结果，总计1.5万笔订单，根据胜率和盈亏比的数值，最终计算的期望值大于0，约为0.7美元。看起来0.7的期望值非常小，但这对于短线交易来说已经非常难得。

当我们引入期望值的概念后，事情变得清晰起来：胜率和盈亏比都不重要，交易中最重要的是期望值。期望值为正，即便绝对值很小，也可以通过成年累月的积累，获得丰厚的收益。

如果期望值为负，即便胜率高达90%以上，也无法在长期内获得正收益。需要提醒的是，市面上可见的大部分交易策略，无论看起来多么高深，其期望值均为负值。只有少部分策略的期望值为零，能够实现正期望值的可谓万中无一。所以，初出茅庐者需要擦亮双眼，避免被看似优秀的“高胜率”策略蒙蔽。

本文转自ATFX官方公众号《ATFX中文服务》风险提示、免责条款、特别声明：

市场有风险，投资需谨慎。以上内容仅代表分析师个人观点，不构成任何操作建议。请勿将本报告视为唯一参考依据。在不同时期，分析师的观点可能发生变化，更新内容不会另行通知。